Solving a Mini Sudoku in 6502 Assembly
Mini-Sudoku meets the 6502
A mini-Sudoku is a simplified variant of the classic Sudoku puzzle. Instead of a 9×9 grid, it consists of a 4×4 board, subdivided into four 2×2 houses. The rules are the same in spirit but smaller in scale:
- Every row, column, and 2×2 house must contain each digit from 1 to 4 exactly once.
- Empty cells are typically represented by zeros.
Because of their small size, mini-Sudokus are usually easy to solve by hand and trivial for modern computers. Precisely for that reason, they make an excellent playground for experimenting with low-level algorithms—and, in this case, for writing a complete solver in 6502 assembly.
The figure below shows an example of such a puzzle: on the left an unsolved mini-Sudoku, and on the right the correctly solved board.
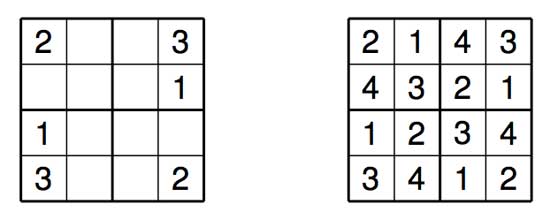
The goal of this post is to explain how a recursive backtracking Sudoku solver can be implemented entirely in 6502 assembly, and how the result can be inspected and verified using an emulator.
Design notes before writing any code
Before diving into assembly, I wrote down a few guiding design decisions. These notes shaped the overall structure of the program and helped keep the implementation manageable despite the limitations of the 6502.
- The Sudoku board is stored as a one-dimensional array of 16 cells, laid out in row-major order.
- A pointer is used to reference the initial input Sudoku, so that different puzzles can be solved without changing the solver logic.
- An initialization routine copies the input puzzle into a working array. The solver only ever modifies this copy, never the original puzzle.
- The core of the program is a recursive
solveroutine implementing a classic backtracking algorithm:- Find the next empty cell.
- Try all possible digits (1–4).
- Check whether the current board state is still legal.
- Recurse until either a solution is found or all options are exhausted.
- A dedicated subroutine checks whether the current board configuration is legal, i.e. contains no duplicate digits in any row, column, or house.
- Another subroutine checks whether the board is completely filled. If the board is full and legal, a solution has been found.
- As soon as a valid solution is detected, the recursion unwinds immediately, leaving the solved board in memory.
- If no solution exists, the solver terminates without modifying the original puzzle.
These constraints lead naturally to a clean separation between data, control flow, and validation logic, even at the assembly level.
Running and inspecting the program
To develop and test the solver, I used a browser-based 6502 emulator created by Michal Kowalski, which has since been extended and improved by the community:
https://sbc.rictor.org/kowalski.html
Originally written many years ago, this simulator aims to faithfully emulate the MOS 6502 and related variants. Over time, its cycle counting and corner cases were refined, making it a surprisingly solid tool for experimenting with non-trivial assembly programs such as this one.
The screenshot below shows the emulator interface used during development.
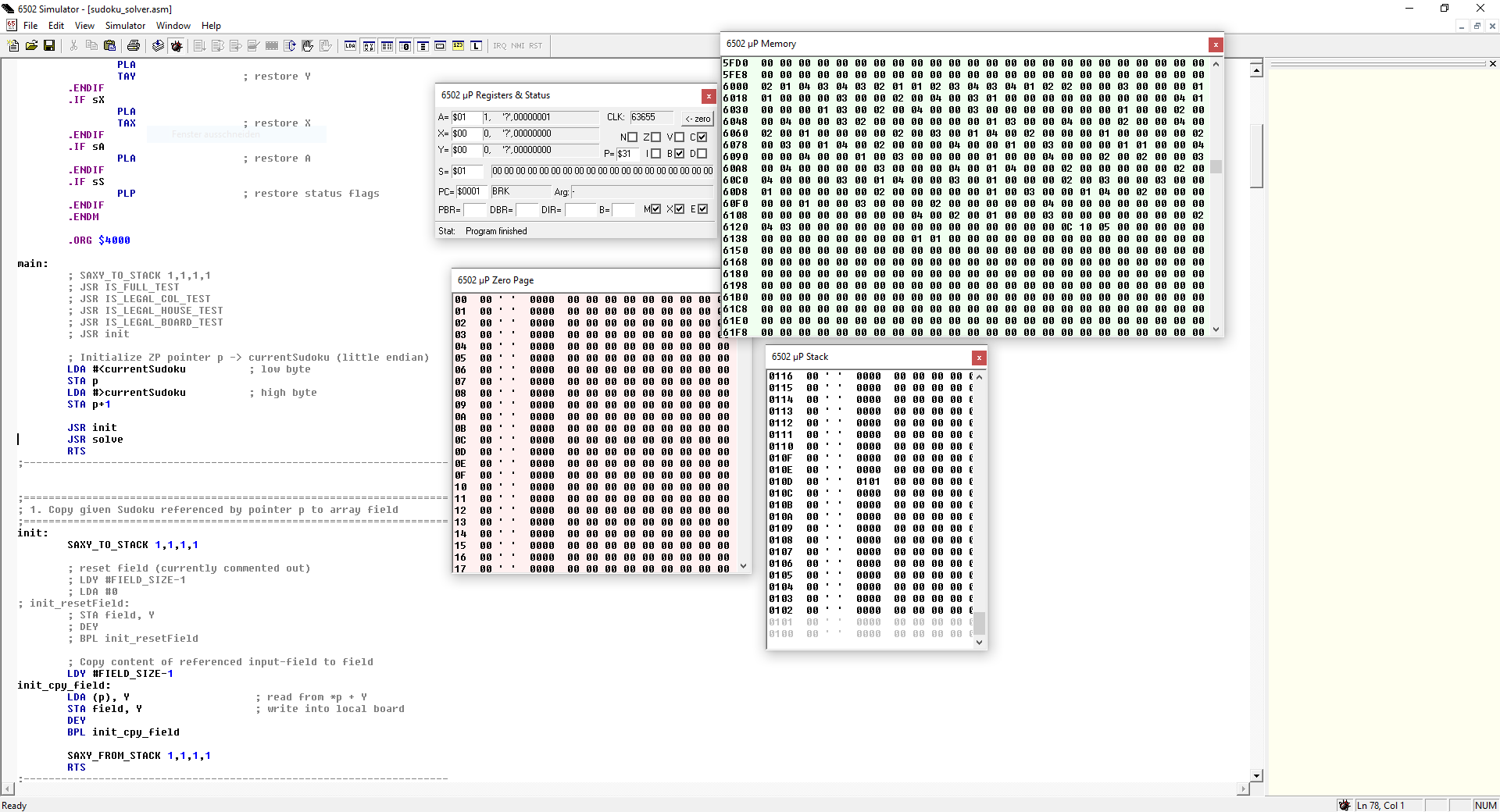
High-level structure of the solver
At a high level, the assembly program proceeds in the following steps:
- Select an input puzzle by pointing to a specific Sudoku stored in memory.
- Initialize the working board by copying the puzzle into a dedicated array.
- Invoke the recursive solver, which:
- Scans for empty cells,
- Tries candidate digits,
- Validates partial solutions,
- Backtracks when necessary.
- Terminate once either:
- A valid solution has been found, or
- All possibilities have been exhausted.
Rather than returning the solved board explicitly, the solver writes the result in place into the working board array. This is both efficient and idiomatic on the 6502, where copying memory is relatively expensive.
Inspecting the Sudoku in memory
One of the advantages of working in an emulator is that memory can be inspected directly.
The next screenshot shows the memory region corresponding to the unsolved mini-Sudoku, right after initialization and before the solver has run.

After the solver completes successfully, the same memory region contains the fully solved board, as shown below.

Reading the memory sequentially from top to bottom corresponds directly to reading the Sudoku row by row.
If you want to experiment further, you can easily adapt the program to solve a different mini-Sudoku by selecting another puzzle in the data section. The solver itself remains unchanged.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
433
434
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
450
451
452
453
454
455
456
457
458
459
460
461
462
463
464
465
466
467
468
469
470
471
472
473
474
475
476
477
478
479
480
481
482
483
484
485
486
487
488
489
490
491
492
493
494
495
496
497
498
499
500
501
502
503
504
505
506
507
508
509
510
511
512
513
514
515
516
517
518
519
520
521
522
523
524
525
526
527
528
529
530
531
532
533
534
535
536
537
538
539
540
541
542
543
544
545
546
547
548
549
550
551
552
553
554
555
556
557
558
559
560
561
562
563
564
565
566
567
568
569
570
571
572
573
574
575
576
577
578
579
580
581
582
583
584
585
586
587
588
589
590
591
592
593
594
595
596
597
598
599
600
601
602
603
604
605
606
607
608
609
610
611
612
613
614
615
616
617
618
619
620
621
622
623
624
625
626
627
628
629
630
631
632
633
634
635
636
637
638
639
640
641
642
643
644
645
646
647
648
649
650
651
652
653
654
655
656
657
658
659
660
661
662
663
; Field is stored in a 1-dim. array (indices)
;|-----------------|
;| 00, 01 | 02, 03 |
;| 04, 05 | 06, 07 |
;|--------+--------|
;| 08, 09 | 10, 11 |
;| 12, 13 | 14, 15 |
;|-----------------|
; --------------------------------------------------------------------
; Zero-page pointer + constants
; --------------------------------------------------------------------
p = $80 ; ZP pointer to current Sudoku (low/high at p, p+1)
FIELD_SIZE = 16
CELLS_PER_ROW = 4
CELLS_PER_COL = 4
NUM_DIGITS = 4
currentSudoku = sudoku17 ; default puzzle source (can be repointed)
;====================================================================
; Macros
;====================================================================
; Save selected registers/flags to stack (order matters!)
SAXY_TO_STACK .MACRO sS, sA, sX, sY
.IF sS
PHP ; save status flags
.ENDIF
.IF sA
PHA ; save A
.ENDIF
.IF sX
TXA ; push X via A
PHA
.ENDIF
.IF sY
TYA ; push Y via A
PHA
.ENDIF
.ENDM
; Restore selected registers/flags from stack (reverse order!)
SAXY_FROM_STACK .MACRO sS, sA, sX, sY
.IF sY
PLA
TAY ; restore Y
.ENDIF
.IF sX
PLA
TAX ; restore X
.ENDIF
.IF sA
PLA ; restore A
.ENDIF
.IF sS
PLP ; restore status flags
.ENDIF
.ENDM
.ORG $4000
main:
; SAXY_TO_STACK 1,1,1,1
; JSR IS_FULL_TEST
; JSR IS_LEGAL_COL_TEST
; JSR IS_LEGAL_HOUSE_TEST
; JSR IS_LEGAL_BOARD_TEST
; JSR init
; Initialize ZP pointer p -> currentSudoku (little endian)
LDA #<currentSudoku ; low byte
STA p
LDA #>currentSudoku ; high byte
STA p+1
JSR init
JSR solve
RTS
;--------------------------------------------------------------------
;====================================================================
; 1. Copy given Sudoku referenced by pointer p to array field
;====================================================================
init:
SAXY_TO_STACK 1,1,1,1
; reset field (currently commented out)
; LDY #FIELD_SIZE-1
; LDA #0
; init_resetField:
; STA field, Y
; DEY
; BPL init_resetField
; Copy content of referenced input-field to field
LDY #FIELD_SIZE-1
init_cpy_field:
LDA (p), Y ; read from *p + Y
STA field, Y ; write into local board
DEY
BPL init_cpy_field
SAXY_FROM_STACK 1,1,1,1
RTS
;--------------------------------------------------------------------
;====================================================================
; Solve the Sudoku given in the array "field"
; Parameters:
; None
; Return:
; AKKU: True(1) if Sudoku could be solved, otherwise False (0)
; Alternative is the Zero-Flag
; Temporary variables used:
; none
;====================================================================
solve:
SAXY_TO_STACK 0,0,1,1 ; only save X/Y
; Two bytes of local state are kept on the stack:
; $0102,X : current index (cell)
; $0101,X : current digit guess
LDA #0
PHA ; start at index 0
PHA ; digit (initially 0)
; If board is full => solved (note: is_full returns 1 by INC on stack)
JSR is_full
BEQ solve_nextCell
; We have a solution
SEC
BCS solveEnd ; unconditional (SEC sets C)
solve_nextCell: ; loop over cells
TSX
LDA $0102, X ; load index (cell pointer) from stack frame
TAY
; Skip filled cells
LDA field, Y
BNE solve_nextCellEnd ; continue with next cell if not empty
; Start trying digits at 1
LDA #1
STA $0101, X ; store current digit in stack frame
solve_nextDigit:
STA field, Y ; set current cell to current digit
; Check legality of this placement (row/col/house + empties allowed)
JSR isLegalBoard
BEQ solve_nextDigitEnd ; not legal => try next digit
; Recurse
JSR solve
SEC ; use Carry as "solution found" indicator
BNE solveEnd ; if solution found (A!=0), stop unwinding
solve_nextDigitEnd:
; Next digit
INC $0101, X
LDA $0101, X
CMP #NUM_DIGITS+1
BMI solve_nextDigit
; No digit worked -> reset cell
LDA #0
STA field, Y
; All digits were tried
CLC ; indicate failure via Carry
BEQ solveEnd ; unconditional (Z is set from previous STA? kept as-is)
solve_nextCellEnd:
INC $0102, X ; next cell index
LDA #FIELD_SIZE
CMP $0102, X
BPL solve_nextCell
CLC ; C-Flag needed to decide on return value
solveEnd:
PLA ; pop index-counter
PLA ; pop digit-counter
SAXY_FROM_STACK 0,0,1,1
LDA #0 ; default return: no solution
BCC solveEndNoSolution ; if Carry clear => failure
LDA #1 ; success
solveEndNoSolution:
RTS
;--------------------------------------------------------------------
;====================================================================
; Check if the whole board is legal (all houses/cols/rows).
; Empty cells are considered legal.
; Parameters:
; None
; Return:
; AKKU: True(1) or False (0), Alternative is the Zero-Flag
; Temporary variables used:
; return+1: Return-value (safe temp; not used by callees)
;====================================================================
isLegalBoard:
SAXY_TO_STACK 0,1,1,1
LDA #0
STA return+1 ; return+1 is not used by called subroutines
LDX #3 ; iterate over 0..3
isLegalBoardLoop:
TXA
JSR isLegalHouse
BEQ isLegalBoardEnd
TXA
JSR isLegalCol
BEQ isLegalBoardEnd
TXA
JSR isLegalRow
BEQ isLegalBoardEnd
DEX
BPL isLegalBoardLoop
INC return+1 ; all checks passed
isLegalBoardEnd:
SAXY_FROM_STACK 0,1,1,1
LDA return+1
RTS
;--------------------------------------------------------------------
;====================================================================
; Check if the given house (0-3) is legal.
; Empty cells are considered as legal.
; Parameters:
; AKKU: House to be checked
; Return:
; AKKU: True(1) or False (0), Alternative is the Zero-Flag
; Temporary variables used:
; return: Return-value
; counter: Offset/temporary
;====================================================================
;|-----------------|
;| 00, 01 | 02, 03 |
;| 04, 05 | 06, 07 |
;|--------+--------|
;| 08, 09 | 10, 11 |
;| 12, 13 | 14, 15 |
;|-----------------|
isLegalHouse:
SAXY_TO_STACK 0,1,1,1
LDA #0
STA counter ; offset for even houses
STA return
; Get house index from caller stack frame
TSX
LDA $0103, X
; Compute starting index of the 2x2 house:
; - LSR splits even/odd house in row (C=1 for odd)
; - ASL*3 scales to row-block offset
LSR ; C-Flag set for odd house
BCC isLegalHouse_EvenHouse
INC counter
INC counter ; Add offset of 2 for odd house
isLegalHouse_EvenHouse:
ASL
ASL
ASL
ADC counter
; Starting index now in A
TAX ; X = start of house
TAY
; Precompute the other 3 indices of this house into counter..counter+2
INY
STY counter ; cell #2
INY
INY
INY
STY counter+1 ; cell #3
INY
STY counter+2 ; cell #4
; Compare cell #1 against the other three (skip if empty)
LDY counter
LDA field, X
BEQ isLegalHouse_EvenHouse_Cell2
CMP field, Y
BEQ isLegalHouseEnd ; #1 == #2
LDY counter+1
CMP field, Y
BEQ isLegalHouseEnd ; #1 == #3
INY
CMP field, Y
BEQ isLegalHouseEnd ; #1 == #4
isLegalHouse_EvenHouse_Cell2:
; Compare cell #2 against #3/#4
INX
LDA field, X
BEQ isLegalHouse_EvenHouse_Cell3
LDY counter+2
CMP field, Y
BEQ isLegalHouseEnd ; #2 == #4
DEY
CMP field, Y
BEQ isLegalHouseEnd ; #2 == #3
isLegalHouse_EvenHouse_Cell3:
; Compare cell #3 against #4
LDY counter+1
LDA field, Y
BEQ isLegalHouseTrue
INY
CMP field, Y
BEQ isLegalHouseEnd ; #3 == #4
isLegalHouseTrue:
INC return
isLegalHouseEnd:
SAXY_FROM_STACK 0,1,1,1
LDA return
RTS
;--------------------------------------------------------------------
;====================================================================
; Check if the given column (0-3) is legal (no duplicates).
; Empty cells are considered as legal.
; Parameters:
; AKKU: Column to be checked
; Return:
; AKKU: True(1) or False (0), Alternative is the Zero-Flag
; Temporary variables used:
; return: Return-value
; counter: loop-counter outer-loop / starting index
; counter+1: loop-counter inner-loop
; index: second-last index of current column
; index+1: last index of current column
;====================================================================
;|-----------------|
;| 00, 01 | 02, 03 |
;| 04, 05 | 06, 07 |
;|--------+--------|
;| 08, 09 | 10, 11 |
;| 12, 13 | 14, 15 |
;|-----------------|
isLegalCol:
SAXY_TO_STACK 0,1,1,1
; Set return value, initially zero
LDA #0
STA return
; Get starting index (column number) from caller stack frame
TSX
LDA $0103, X
STA counter
; calc second-last index of current column
CLC
ADC #CELLS_PER_ROW*2
STA index ; second-last index of current column
; calc last index of current column
ADC #CELLS_PER_ROW
STA index+1 ; last index of current column
; <outerLoop>
isLegalCol_checkLoop:
CLC
LDA counter
TAY
ADC #CELLS_PER_ROW
STA counter+1
; <innerLoop> compare field[Y] against all later cells in this column
isLegalCol_countDigits:
LDX counter+1
LDA field, Y
BEQ isLegalCol_checkLoopEnd ; empty => skip comparisons
CMP field, X
BEQ isLegalColEnd ; duplicate found => illegal
CLC
LDA counter+1
ADC #CELLS_PER_ROW
STA counter+1
LDA index+1
CMP counter+1
BCS isLegalCol_countDigits
; </innerLoop>
isLegalCol_checkLoopEnd:
CLC
LDA counter
ADC #CELLS_PER_ROW
STA counter
LDA index
CMP counter
BCS isLegalCol_checkLoop
; </outerLoop>
INC return ; no duplicates
isLegalColEnd:
SAXY_FROM_STACK 0,1,1,1
LDA return
RTS
;====================================================================
; Check if the given row (0-3) is legal (no duplicates).
; Empty cells are considered as legal.
; Parameters:
; AKKU: Row to be checked
; Return:
; AKKU: True(1) or False (0), Alternative is the Zero-Flag
; Temporary variables used:
; index: starting index of next row
; index+1: last index of current row
; return: Return-value
;====================================================================
;|-----------------|
;| 00, 01 | 02, 03 |
;| 04, 05 | 06, 07 |
;|--------+--------|
;| 08, 09 | 10, 11 |
;| 12, 13 | 14, 15 |
;|-----------------|
isLegalRow:
SAXY_TO_STACK 0,1,1,1
; Set return value, initially zero
LDA #0
STA return
; Multiply row by 4 to get starting index
TSX
LDA $0103, X
ASL
ASL
TAX ; X = row start (outer loop)
; Add 4 to get first index of the next row
CLC
ADC #CELLS_PER_ROW
STA index
; Add 3 to get last index of current row
STA index+1
DEC index+1
; <Outer loop> iterate over cells in this row
isLegalRow_checkLoop:
TXA
TAY ; Y = current cell (inner loop anchor)
INY ; start comparisons at next cell
LDA field, X ; digit to check
BEQ isLegalRow_CheckLoopEnd ; empty => skip comparisons
; <Inner loop> compare against remaining cells in row
isLegalRow_countDigits:
CMP field, Y
BEQ isLegalRow_End ; duplicate found
INY
CPY index
BNE isLegalRow_countDigits
; </Inner loop>
isLegalRow_CheckLoopEnd:
INX
CPX index+1
BNE isLegalRow_checkLoop
; </Outer loop>
INC return ; no duplicates
isLegalRow_End:
SAXY_FROM_STACK 0,1,1,1
LDA return
RTS
;====================================================================
; Tests if the sudoku-field is completely filled.
; Does NOT check consistency: only whether every cell != 0.
; Return is via stack-mutation trick (INC $0103,X) while A stays 0/1.
; Zero flag can be used by caller.
;====================================================================
is_full:
LDA #0 ; assume not full (return value 0)
SAXY_TO_STACK 0,1,1,1
LDX #FIELD_SIZE-1
is_full_loop:
; Check if cell is empty and leave loop if so
LDY field, X
BEQ is_full_end
; Cell not empty -> next
DEX
BPL is_full_loop ; continue while X >= 0
; All cells filled -> set return-value to true (1)
TSX
INC $0103, X ; flips caller-visible return byte
is_full_end:
SAXY_FROM_STACK 0,1,1,1
RTS
;--------------------------------------------------------------------
;====================================================================
; Data section
;====================================================================
.ORG $6000
; --------------------------------------------------------------------
; Working field (4x4 Sudoku = 16 cells)
; This is the board that gets modified by the solver
; --------------------------------------------------------------------
field:
.RS $10 ; reserve 16 bytes for the current board
; --------------------------------------------------------------------
; Sudoku test boards (4x4)
; Zeros denote empty cells
; Comments show one valid solution (if solvable)
; --------------------------------------------------------------------
sudoku17:
ll171: .BYTE 2,0,0,3 ; 2,4,1,3
ll172: .BYTE 0,0,0,1 ; 1,3,2,4
ll173: .BYTE 1,0,0,0 ; 4,1,3,2
ll174: .BYTE 3,0,0,2 ; 3,2,4,1
sudoku16:
ll161: .BYTE 0,4,0,3 ; 2,4,1,3
ll162: .BYTE 1,0,0,0 ; 1,3,2,4
ll163: .BYTE 0,0,0,0 ; 4,1,3,2
ll164: .BYTE 0,0,4,1 ; 3,2,4,1
sudoku15:
ll151: .BYTE 0,0,0,1 ; 2,4,3,1
ll152: .BYTE 3,0,2,0 ; 3,1,2,4
ll153: .BYTE 4,0,0,3 ; 4,2,1,3
ll154: .BYTE 0,0,0,0 ; 1,3,4,2
sudoku14:
ll141: .BYTE 0,0,0,1 ; 2,3,4,1
ll142: .BYTE 0,0,2,0 ; 4,1,2,3
ll143: .BYTE 0,4,0,0 ; 1,4,3,2
ll144: .BYTE 3,2,0,0 ; 3,2,1,4
sudoku13:
ll131: .BYTE 0,0,0,0 ; 2,4,1,3
ll132: .BYTE 1,3,0,0 ; 1,3,2,4
ll133: .BYTE 4,0,0,2 ; 4,1,3,2
ll134: .BYTE 0,0,4,0 ; 3,2,4,1
sudoku12:
ll121: .BYTE 2,0,1,0 ; not solvable
ll122: .BYTE 0,0,0,2
ll123: .BYTE 0,3,0,1
ll124: .BYTE 4,0,2,0
sudoku11:
ll111: .BYTE 0,0,1,0 ; 3,2,1,4
ll112: .BYTE 0,0,0,2 ; 1,4,3,2
ll113: .BYTE 0,3,0,1 ; 2,3,4,1
ll114: .BYTE 4,0,2,0 ; 4,1,2,3
sudoku10:
ll101: .BYTE 0,0,4,0 ; not solvable
ll102: .BYTE 0,1,0,3
ll103: .BYTE 0,0,0,1
ll104: .BYTE 1,0,0,4
sudoku9:
ll91: .BYTE 0,0,4,0 ; 2,3,4,1
ll92: .BYTE 0,1,0,3 ; 4,1,2,3
ll93: .BYTE 0,0,0,0 ; 3,4,1,2
ll94: .BYTE 1,0,0,4 ; 1,2,3,4
sudoku8:
ll81: .BYTE 0,0,2,0 ; 4,3,2,1
ll82: .BYTE 2,0,0,3 ; 2,1,4,3
ll83: .BYTE 0,4,0,0 ; 3,4,1,2
ll84: .BYTE 0,0,3,0 ; 1,2,3,4
sudoku7:
ll71: .BYTE 0,0,4,0 ; 3,2,4,1
ll72: .BYTE 1,4,0,0 ; 1,4,3,2
ll73: .BYTE 2,0,0,0 ; 2,3,1,4
ll74: .BYTE 0,0,2,0 ; 4,1,2,3
sudoku6:
ll61: .BYTE 4,0,0,0 ; 4,1,2,3
ll62: .BYTE 3,0,1,4 ; 3,2,1,4
ll63: .BYTE 0,0,3,0 ; 2,4,3,1
ll64: .BYTE 1,0,0,0 ; 1,3,4,2
sudoku5:
ll51: .BYTE 2,0,3,0 ; 2,1,3,4
ll52: .BYTE 0,3,0,0 ; 4,3,1,2
ll53: .BYTE 1,0,0,0 ; 1,2,4,3
ll54: .BYTE 0,0,2,0 ; 3,4,2,1
sudoku4:
ll41: .BYTE 0,0,0,0 ; 4,3,2,1
ll42: .BYTE 1,0,3,0 ; 1,2,3,4
ll43: .BYTE 0,1,4,0 ; 3,1,4,2
ll44: .BYTE 2,0,0,0 ; 2,4,1,3
sudoku3:
ll31: .BYTE 0,0,1,0 ; 2,4,1,3
ll32: .BYTE 0,3,0,0 ; 1,3,4,2
ll33: .BYTE 0,2,0,0 ; 4,2,3,1
ll34: .BYTE 0,0,0,4 ; 3,1,2,4
sudoku2:
ll21: .BYTE 0,0,0,0
ll22: .BYTE 0,0,0,0
ll23: .BYTE 0,0,0,0
ll24: .BYTE 0,0,0,0
sudoku1:
ll11: .BYTE 4,0,2,0 ; 4,3,2,1
ll12: .BYTE 1,0,0,3 ; 1,2,4,3
ll13: .BYTE 0,0,0,0 ; 2,1,3,4
ll14: .BYTE 0,0,0,2 ; 3,4,1,2
; --------------------------------------------------------------------
; Temporary variables
; NOTE:
; - Only valid within ONE subroutine
; - Must not be relied upon across subroutine calls
; - Contents are generally non-zero / undefined on entry
; --------------------------------------------------------------------
index: .RS $10 ; general-purpose index storage
counter: .RS $10 ; loop counters / offsets
return: .RS $10 ; boolean return values
Appendix
I also wrote a bunch of tests for the code which are listed here.
Enjoy Reading This Article?
Here are some more articles you might like to read next: